La representación de los objetos en tres dimensiones
sobre una superficie plana, de manera
que ofrezcan una sensación de volumen se
llama Perspectiva. Se representan
los objetos sobre tres ejes XYZ. En el eje Z,
se representa la altura. En el eje Y, se representa la anchura y en el
eje X, se representa la longitud.
Los distintos
tipos de perspectivas dependen de la inclinación de los planos Los sistema más utilizados son la
isométrica, la caballera y la cónica.
Estudiaremos en este curso las dos primeras.
Perspectiva Isométrica. En ella los ejes quedan separados
por un mismo ángulo (120º). Las medidas
siempre se refieren a los tres ejes que tienen su origen en un único punto.
Perspectiva Caballera. En ella los ejes X y Z tienen un ángulo de 90º y el eje Y con respecto a Z tiene una inclinación
de 135º. En es te caso las medidas en los ejes X y Z son las reales y las del
eje Y tiene un coeficiente de reducción
de 0.5.
DIBUJAR EN PERSPECTIVA
En ambas perspectivas, el sistema más sencillo es llevar
las tres vistas principales sobre los
planos formados por los ejes:
Alzado en el
plano XZ.
Planta en el
plano XY.
Perfil en el
plano YZ.
Cada una de las aristas que forman las vistas se prolonga
paralelamente al eje que corresponda:
Horizontal
paralelo al eje de las X.
Vertical
paralelo al eje de las Z.
Profundidad
paralelo al eje de las Y
Transformaciones en OpenGL
En algunos tutoriales anteriores de OpenGL se han
mencionado de manera fragmentaria los conceptos de transformaciones:
· En los
“Hola Mundo 3d en OpenGL” y “Hola Complicado Mundo OpenGL-win32” se utilizaron
algunas transformaciones de proyección y viewport para ajustar la
inicialización de la ventana, pero sin entrar mucho en detalle acerca de su
funcionamiento.
Este tutorial explora los diferentes tipos de transformaciones
en OpenGL, a saber:
·
Proyección: Trasforman una escena 3d “abstracta”, en una imagen plana
que puede ser visualizada en una pantalla.
· Viewport:
Ajustan el producto de la proyección a las dimensiones de un rectángulo contenedor
(ventana).
· De vista:
Que definen y afectan la posición desde la cual se visualizan las escenas
tridimensionales.
· Modelado:
Sirven para manipular los objetos en la escena, permitiendo trasladarlos,
rotarlos y deformarlos (escalarlos).
·
Modelo-Vista: Son la combinación de las dos transformaciones anteriores,
que desde un punto de vista práctico son semejantes.
· void
glMatrixMode( enum mode ); Permite seleccionar la matriz sobre la cual se
realizaran las operaciones, los posibles valores de mode son TEXTURE,
MODELVIEW, COLOR o PROJECTION . Por ahora las más interesantes son MODELVIEW y
PROJECTION, las otras se verán en su momento.
· Void
glLoadMatrix{fd} (T m[16]); Recibe una matriz de 4×4 que reemplaza la actual
seleccionada. El arreglo es ordenado en forma de una matriz que tiene orden Y,
a diferencia de las matrices convencionales que tienen orden X, lo que quiere
decir que tiene la forma.
· void
glMultMatrix{fd}( T m[16] ); Multiplica la matriz actual por la matriz m[16] y
reemplaza la matriz actual con el resultado de la operación. La operación
resultante sería algo así como A’ = A M , donde A es la matriz actual, M es la
matriz suministrada y A’ es la nueva matriz que resulta de la operación y que
reemplaza a A.
· void
glLoadTransposeMatrix{fd}( T m[16] ); Realiza una función similar a
LoadMatrix(), con la diferencia que trabaja sobre una matriz en orden X así.
· void
glMultTransposeMatrix{fd}( T m[16] ); Misma funcionalidad que MultMatrix() ,
solo que actúa en base al la matriz en orden X, o sea la transpuesta.
· void
glLoadIdentity( void ); Remplaza la matriz actual por la matriz identidad de
tamaño 4×4.
Estas operaciones afectan directamente las matrices
mencionadas anteriormente, debido a que las operaciones de “alto nivel”
(trasladar, rotar, escalar) que existen mas adelante se concatenan, es decir su
efecto se acumula sobre matriz actual, existen dos operaciones que permiten
guardar la matriz actual en una pila y restaurarla cuando sea necesario, estas
son:
· void
glPushMatrix( void ); Coloca una copia de la matriz actual en la parte superior
de la pila correspondiente.
· void
glPopMatrix( void ); Saca el elemento superior de la pila, que pasa a
reemplazar a la matriz actual.
Estas dos operaciones son muy utilizadas, debido a que
permiten realizar transformaciones sobre objetos diferentes, manteniendo
algunas de las anteriores sin modificar.
Proyección
Como ya se ha visto en tutoriales anteriores, OpenGL
maneja 2 tipos de proyección, en perspectiva y ortográfica, donde la primera
corresponde a la visión “realista” de la escena, mientras que la segunda es una
“plana” que no deforma las dimensiones de los objetos dependiendo de su
distancia a la cámara.
Ortográfica: Para ajustar la proyección ortográfica se
utiliza el siguiente grupo de funciones:
glOrtho(GLdouble
left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble
far);
gluOrtho2D(GLdouble
left, GLdouble right, GLdouble bottom, GLdouble top);
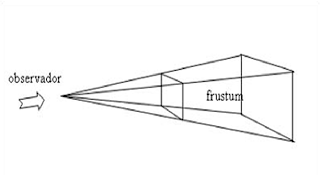
Perspectiva: Existen dos manera de manejar la proyección
en perspectiva, a través de de una función gl o mediante la librería glu (una
tercera puede ser realizar los cálculos de la matriz “manualmente”. En el primer caso:
glFrustrum(GLdouble
left, GLdouble right, GLdouble bottom, GLdouble top, GLdouble near, GLdouble
far)
Transformaciones ModelView
Una tarea muy común en la creación de gráficos 2d, 3d y
videojuegos es la de mover objetos par crear cierta animación. La primera idea
que se nos viene a la cabeza en el caso de OpeGL es que todo modelo está
formado por primitivas, toda primitiva por puntos y finalmente todo punto por
una tripleta de coordenadas XYZ, así que si se cambian las coordenadas todo de
ahí hacia arriba se mueve.
void glRotate[fd](GLfloat
angle, GLfloat x, GLfloat y, GLfloat z);
Hay que tener en cuenta las siguientes características a
la hora de utilizar estas funciones:
· Estas
tres operaciones afectan la matriz actual seleccionada, bien sea MODELVIEW o
PROJECTION, generalmente para propósitos de rotar objetos dentro de la escena
se utiliza la matriz MODELVIEW.
· El eje
coordenado de referencia para las operaciones tanto en MODELVIEW como en
PROJECTION se denomina “eye coordinates”, que traduce coordenadas de “ojo” o
mejor “vista”. Este es un sistema inamovible y en ausencia de cualquier
transformación, la “cámara” está situada en (0,0,0) apuntando hacia la
dirección Z negativa, con el vector “arriba” en el sentido Y positivo.
· Cada
operación que afecta la matriz MODELVIEW crea otro sistema coordenado para los
objetos que se dibujen después de realizada la trasformación, dicho sistema
difiere del “básico”, es decir de las llamadas coordenadas de vista (eye
coordinates) dependiendo de todo el conjunto de transformaciones realizadas
desde el momento en que la matriz MODELVIEW dejo de ser la identidad.
· Una
consecuencia de lo anterior es que las operaciones no son conmutativas, es
decir que un llamado de glRotatef(), seguido de uno de glTranslatef() produce
un efecto diferente a llamar las operaciones en orden inverso. Esto se ve mejor
ilustrado en el gráfico:
· Es
importante aprender a utilizar correctamente glPushMatrix(), glPopMatrix() y
otras operaciones que permitan salvar y restaurar estados de matriz, debido a
que permiten realizar translaciones y rotaciones especificas para un cierto
objeto, sin alterar los otros.
Hardware
En realidad, el API de ogl está pensado para trabajar
bajo el respaldo de un hardware capaz de realizar las operaciones necesarias
para el renderizado, pero si no se dispone de ese hardware, estas operaciones
se calcularan por medio de un software contra la CPU del sistema. Así que los
requerimientos hardware son escasos, aunque cuanto mayor sea las capacidades de
la maquina, mayor será el rendimiento de las aplicaciones ogl.
Windows
En principio, cualquier versión de windows viene con las
librerías necesarias para ejecutar cualquier aplicación que utilice OpenGL.
Para el desarrollo de las mismas, el Microsoft Visual Studio, y en particular
Visual C++ trae también todo lo necesario. Puedes consegir, además, la última
versión de la GLUT en la web de Nate Robins.
Linux
Para visualizar aplicaciones OpenGL en XFree86
necesitarás instalar un paquete para el soporte de las librerías Mesa (que es
el equivalente en software libre de OpenGL) y de las utilidades GLU y GLUT.
Para realizar desarrollo necesitarás, a mayores, los paquetes equivalentes en
modo dev.
En el caso de la distribución Ubuntu los paquetes
necesarios para desarrollo y visualización son los siguientes:
- Freeglut3-dev
- libgl1-mesa-dev
- libglu1-mesa-dev
- libglut3.dev
Coordenadas oculares
Las coordenadas oculares se sitúan en el punto de vista del observador,
sin importar las transformaciones que tengan lugar. Por tanto, estas
coordenadas representan un sistema virtual de coordenadas fijo usado como marco
de referencia común.
Transformaciones
Las transformaciones son las que hacen posible la proyección de
coordenadas 3D sobre superficies 2D. También son las encargadas de mover, rotar
y escalar objetos.
El modelador
En esta sección se recogen las transformaciones del observador y del
modelado puesto que, como se verá en el apartado, constituyen, al fin y al
cabo, la misma transformación.
Transformaciones del observador
La transformación del observador es la primera que se aplica a la
escena, y se usa para determinar el punto más ventajoso de la escena. Por
defecto, el punto de vista está en el origen (0,0,0) mirando en dirección
negativa del eje z. La transformación del observador permite colocar y apuntar
la cámara donde y hacia donde se quiera.
Transformaciones del modelo
Estas transformaciones se usan para situar, rotar y escalar los objetos
de la escena. La apariencia final de los objetos depende en gran medida del
orden con el que se hayan aplicado las transformaciones.
Transformaciones
de la proyección
La transformación de proyección se aplica a la
orientación final del modelador. Esta proyección define el volumen de
visualización y establece los planos de trabajo
Los dos tipos de proyección más utilizados son
la ortográfica y la perspectiva, que veremos más adelante.
Transformaciones
de la vista
En el momento en que se ha terminado todo el
proceso de transformaciones, solo queda un último paso: proyectar lo que hemos
dibujado en 3D al 2D de la pantalla, en la ventana en la que estamos
trabajando.
Matrices
Las matemáticas que hay tras estas
transformaciones se simplifican gracias a las matrices. Cada una de las
transformaciones de las que se acaba de hablar puede conseguirse multiplicando
una matriz que contenga los vértices por una matriz que describa la
transformación.
El
canal de transformaciones
Para poder llevar a cabo
todas las transformaciones de las que se acaba de hablar, deben modificarse dos
matrices: la matriz del Modelador y la matriz de Proyección.
La
matriz del modelador
La matriz del modelador es
una matriz 4x4 que representa el sistema de coordenadas transformado que se
está usando para colocar y orientar los objetos.
La
matriz de proyección
La matriz de proyección
especifica el tamaño y la forma del volumen de visualización. El volumen de
visualización es aquel cuyo contenido es el que se representa en pantalla.
Proyecciones
ortográficas
Una proyección ortográfica
es cuadrada en todas sus caras. Esto produce una proyección paralela, útil para
aplicaciones de tipo CAD o dibujos arquitectónicos, o también para tomar
medidas, ya que las dimensiones de lo que representan no se ven alteradas por
la proyección.
Proyecciones
perspectivas
Una proyección en
perspectiva reduce y estirar los objetos más alejados del observador. Es
importante saber que las medidas de la proyección de un objeto no tienen por
qué coincidir con las del objeto real, ya que han sido defo