Coordenadas
oculares
Las coordenadas oculares se sitúan en el punto de vista
del observador, sin importar las transformaciones que tengan lugar. Por tanto,
estas coordenadas representan un sistema virtual de coordenadas fijo usado como
marco de referencia común.
Transformaciones
También son las encargadas de mover, rotar y escalar
objetos. En realidad, estas transformaciones no se aplican a los modelos en sí,
si no al sistema de coordenadas, de forma que si se quiere rotar un objeto, no
lo se le rota, sino que se rota el eje sobre el que se sitúa.
En esta sección se recogen las transformaciones del
observador y del modelado puesto que, como se verá en el apartado 4.2.1.3,
constituyen, al fin y al cabo, la misma transformación.
Transformaciones
del observador
La transformación del observador es la primera que se
aplica a la escena, y se usa para determinar el punto más ventajoso de la
escena. Por defecto, el punto de vista está en el origen (0,0,0) mirando en
dirección negativa del eje z.
Transformaciones del modelo
Estas transformaciones se usan para situar, rotar y
escalar los objetos de la escena. La apariencia final de los objetos depende en
gran medida del orden con el que se hayan aplicado las transformaciones.
Transformaciones
de la proyección
La transformación
de proyección se aplica a la orientación final del modelador. Esta proyección
define el volumen de visualización y establece los planos de trabajo. A efectos
prácticos, esta translación especifica cómo se traslada una escena finalizada a
la imagen final de la pantalla.
Matrices
Cada una de las
transformaciones de las que se acaba de hablar puede conseguirse multiplicando
una matriz que contenga los vértices por una matriz que describa la
transformación. Por tanto todas las transformaciones ejecutables con ogl pueden
describirse como la multiplicación de dos o más matrices.
El canal de transformaciones
OpenGL proporciona
muchas funciones de alto nivel que hacen muy sencillo la construcción de
matrices para transformaciones. Éstas se aplican sobre la matriz que este
activa en ese instante. Para activar una de las dos matrices utilizamos la
función glMatrixMode. Hay dos parámetros posibles:
glMatrixMode(GL_PROJECTION);
activa la matriz de proyección, y
glMatrixMode(GL_MODELVIEW);
activa la del modelador.
La
matriz del modelador
La matriz del modelador es una matriz 4x4 que representa
el sistema de coordenadas transformado que se está usando para colocar y
orientar los objetos. Si se multiplica la matriz del vértice (de tamaño 1x4)
por ésta se obtiene otra matriz 1x4 con los vértices transformados sobre ese
sistema de coordenadas.
Translación
Imaginemos que se quiere dibujar un cubo con la función
de la librería GLUT glutSolidCube, que lleva como parámetro el lado del cubo.
Si se escribe el siguiente código:
glutSolidCube(5);
se obtiene un cubo centrado en el origen (0,0,0) y con el
lado de la arista 5.
glTranslatef(10.0f,
0.0f, 0.0f);
glutSolidCube(5);
La “f” añadida a la función indica que se usarán
flotantes. Los parámetros de glTranslate son las unidades a desplazar en el eje
x, y y z, respectivamente. Pueden ser valores negativos, para trasladar en el
sentido contrario.
Rotación
Para rotar, tenemos también una función de alto nivel que
construye la matriz de transformación y la multiplica por la matriz activa,
glRotate. Lleva como parámetros el ángulo a rotar (en grados, sentido horario),
y después x, y y z del vector sobre el cual se quiere rotar el objeto. Una
rotación simple, sobre el eje y, de 10º sería
glRotatef(10, 0.0f, 1.0f, 0.0f);
Escalado
Una transformación de escala incrementa el tamaño de
nuestro objeto expandiendo todos los vértices a lo largo de los tres ejes por
los factores especificados. La función glScale lleva como parámetros la escala
en x, y y z, respectivamente. El valor 1.0f es la referencia de la escala, de
tal forma que la siguiente línea:
glScalef(1.0f, 1.0f, 1.0f);
no modificaría el objeto en absoluto. Un valor de 2.0f
sería el doble, y 0.5f sería la mitad. Por ejemplo, para ensanchar un objeto a
lo largo de su eje z, de tal forma que quedase cuatro veces más “alargado” en
este eje, sería:
glScalef(1.0f, 1.0f, 4.0f);
La
matriz de proyección
La matriz de proyección especifica el tamaño y la forma
del volumen de visualización. Está delimitado por una serie de planos de
trabajo. De estos planos, los más importantes son los planos de corte, que son
los que nos acotan el volumen de visualización por delante y por detrás. Todo
lo que esté más adelante del plano de corte más alejado de la cámara (zfar) no
se representa.
Proyecciones ortográficas
Una proyección ortográfica es cuadrada en todas sus
caras. Esto produce una proyección paralela, útil para aplicaciones de tipo CAD
o dibujos arquitectónicos, o también para tomar medidas, ya que las dimensiones
de lo que representan no se ven alteradas por la proyección.
Para definir la matriz de proyección ortográfica y
multiplicarla por la matriz activa (que debería ser en ese momento la de
proyección, GL_PROJECTION), se utiliza la función glOrtho, que se define de la
siguiente forma:
glOrtho(limiteIzquierdo, limiteDerecho, limiteAbajo,
limiteArriba, znear, zfar)
siendo todos flotantes.
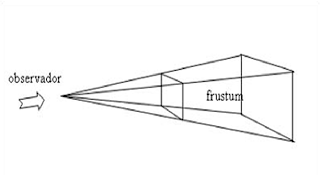
Proyecciones
perspectivas
Una proyección en
perspectiva reduce y estirar los objetos más alejados del observador. Es
importante saber que las medidas de la proyección de un objeto no tienen por
qué coincidir con las del objeto real, ya que han sido deformadas.
Ejemplo:
una escena simple
Código
El siguiente código es un
programa que usa OpenGL mediante la librería GLUT. Primero se lista el código
completo y luego se comenta línea por línea. Con él se aplicará lo aprendido en
el anterior capítulo y el presente, además de nuevas funciones de la librería
GLUT.
#include <GL/glut.h>
GLfloat anguloCuboX = 0.0f;
GLfloat anguloCuboY = 0.0f;
GLfloat anguloEsfera = 0.0f;
GLint ancho=400;
GLint alto=400;
int hazPerspectiva = 0;
void reshape(int width, int height)
{
glViewport(0, 0, width, height);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if(hazPerspectiva)
gluPerspective(60.0f, (GLfloat)width/(GLfloat)height, 1.0f, 20.0f);
else
glOrtho(-4,4, -4, 4, 1, 10);
glMatrixMode(GL_MODELVIEW);
ancho =
width;
alto =
height;
}
void drawCube(void)
{
glColor3f(1.0f, 0.0f, 0.0f);
glBegin(GL_QUADS); //cara
frontal
glVertex3f(-1.0f, -1.0f, 1.0f);
glVertex3f(
1.0f, -1.0f, 1.0f);
glVertex3f(
1.0f, 1.0f, 1.0f);
glVertex3f(-1.0f, 1.0f, 1.0f);
glEnd();
glColor3f(0.0f, 1.0f, 0.0f);
glBegin(GL_QUADS); //cara trasera
glVertex3f( 1.0f, -1.0f, -1.0f);
glVertex3f(-1.0f, -1.0f, -1.0f);
glVertex3f(-1.0f, 1.0f, -1.0f);
glVertex3f(
1.0f, 1.0f, -1.0f);
glEnd();
glColor3f(0.0f, 0.0f, 1.0f);
glBegin(GL_QUADS); //cara
lateral izq
glVertex3f(-1.0f,-1.0f, -1.0f);
glVertex3f(-1.0f,-1.0f, 1.0f);
glVertex3f(-1.0f, 1.0f, 1.0f);
glVertex3f(-1.0f,
1.0f, -1.0f);
glEnd();
glColor3f(1.0f, 1.0f, 0.0f);
glBegin(GL_QUADS); //cara
lateral dcha
glVertex3f(1.0f, -1.0f, 1.0f);
glVertex3f(1.0f, -1.0f, -1.0f);
glVertex3f(1.0f, 1.0f, -1.0f);
glVertex3f(1.0f, 1.0f, 1.0f);
glEnd();
glColor3f(0.0f, 1.0f, 1.0f);
glBegin(GL_QUADS); //cara
arriba
glVertex3f(-1.0f, 1.0f, 1.0f);
glVertex3f(
1.0f, 1.0f, 1.0f);
glVertex3f(
1.0f, 1.0f, -1.0f);
glVertex3f(-1.0f, 1.0f, -1.0f);
glEnd();
glColor3f(1.0f, 0.0f, 1.0f);
glBegin(GL_QUADS); //cara abajo
glVertex3f( 1.0f,-1.0f, -1.0f);
glVertex3f( 1.0f,-1.0f, 1.0f);
glVertex3f(-1.0f,-1.0f, 1.0f);
glVertex3f(-1.0f,-1.0f, -1.0f);
glEnd();
}
void display()
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
glTranslatef(0.0f, 0.0f, -5.0f);
glRotatef(anguloCuboX, 1.0f, 0.0f, 0.0f);
glRotatef(anguloCuboY, 0.0f, 1.0f, 0.0f);
drawCube();
glLoadIdentity();
glTranslatef(0.0f, 0.0f, -5.0f);
glRotatef(anguloEsfera, 0.0f, 1.0f, 0.0f);
glTranslatef(3.0f, 0.0f, 0.0f);
glColor3f(1.0f, 1.0f, 1.0f);
glutWireSphere(0.5f, 8, 8);
glFlush();
glutSwapBuffers();
anguloCuboX+=0.1f;
anguloCuboY+=0.1f;
anguloEsfera+=0.2f;
}
void init()
{
glClearColor(0,0,0,0);
glEnable(GL_DEPTH_TEST);
ancho
= 400;
alto = 400;
}
void idle()
{
display();
}
void keyboard(unsigned char key, int x, int y)
{
switch(key)
{
case 'p':
case 'P':
hazPerspectiva=1;
reshape(ancho,alto);
break;
case 'o':
case 'O':
hazPerspectiva=0;
reshape(ancho,alto);
break;
case 27:
// escape
exit(0);
break;
}
}
int main(int argc, char **argv)
{
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
glutInitWindowPosition(100, 100);
glutInitWindowSize(ancho, alto);
glutCreateWindow("Cubo
1");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutIdleFunc(idle);
glutKeyboardFunc(keyboard);
glutMainLoop();
return
0;
}
1.
¿Puede diferenciar entre los dos tipos de proyección?
La ortogonal aun que
pareciera que es 3D en realidad solo es 2D
tiene un único ángulo de visión y en perspectiva la profundidad con que
se ve la imagen depende del ángulo de visión.
2.
¿Entiende para que se usan las matrices y como las maneja opengl? explíquelo.
Se usan para hacer
operaciones con vectores y dependiendo que se desee lograr se utiliza una
propiedad diferente de las matrices, ya sea rotación, traslación, etc..
3.
¿Qué es la matriz identidad y para que se utiliza en opengl?
Cumple con la propiedad de
ser el elemento neutro del producto de matrices, podría ser utilizada
multiplicándola con un escalar y hacer una estalación con otra matriz vectores
5.
explique las diferencias
La diferencia sería que el
primer cubo sin rotar se ve como si fuera en 2D por que solo se ve una
cara y en perspectiva, ya nos podríamos
dar cuenta de la profundidad del objeto y verlo en 3D


No hay comentarios:
Publicar un comentario